有限元法(FEM)作为一种分析和设计工具,已广泛应用于天线、微波和信号完整性等众多
电子工程领域。FEM求解器与其它矩量法(MoM)和时域有限差分法(FDTD)等数值方法相比拥有多项显着的优势。这些优势包括:能够处理复杂的非均匀和各向异性材料、能够借助四面体单元准确地描绘复杂几何形状、能够使用高阶基函数实现准确性、具有多种端口和入射波等激励方式。利用这些功能优势,FEM就能够以极高的准确性对波导结构进行建模。
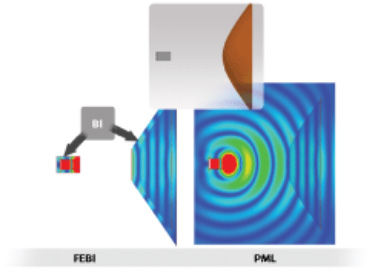
但是,对于开放空间问题(例如天线向开放空间辐射的时候),FEM求解器需要通过在人工截断的边界表面上设定辐射边界条件(RBC),以便将无限域截断为有限域。两种广泛使用的RBC包括一阶吸收边界条件(ABC)和理想匹配层(PML),后者通常情况下都能够提供最佳的准确性。两种方法都保留了FEM系统矩阵的稀疏性,但仅适用于凸起的辐射表面。两种都属于近似方法,都存在准确性问题,比如会产生来自辐射表面的非物理伪反射。这个问题可以通过增大RBC与辐射结构的间距,让反射降至可忽视的水平,来予以解决。
另一方面,积分方程(IE)法,比如MoM,则非常适合对位于匀质边界或无限大介质中的结构进行建模。其分析内核采用格林函数,可以在无穷远处采用Sommerfeld辐射条件。因此,不管是从内存占用,还是从CPU时间占用来说,对多个在空间上分离,互不相连的同质结构,IE求解器都毋庸置疑地成为更好的选择,因为它不需要对目标之间的空间进行详细的建模。
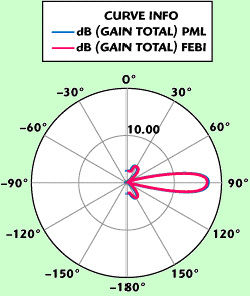
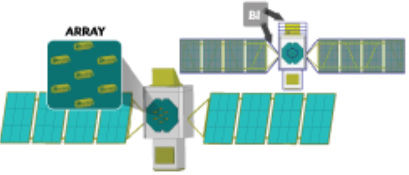
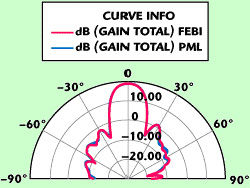
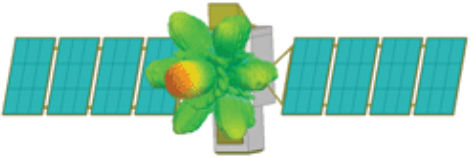
早在1990年,Yuan就已经成功实现了FEM求解器和IE求解器的混合算法,这个方法现普遍称为混合有限元边界积分方法(FEBI)。这种方法把边界积分:Sommerfeld辐射条件的MoM解,用作FEM解的截断边界,因此可以在理论上准确地处理远场辐射条件。这样就引出一系列有意思的特性,比如可用作任意形状的距离辐射体很近的全共形的辐射表面。
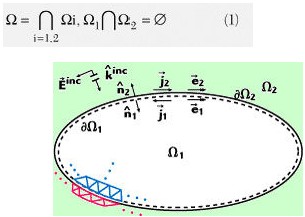
本文将介绍ANSYS公司在HFSS中提供的一款全新的FEBI求解器。该求解器得力于近期区域分解方法的进步。在现有的FEBI方法中,无限未知域被分割为两个互不重叠的域:一个有界FEM域和一个无界同质外部域。两个域间的耦合通过其交界面上的合适的边界条件加以考虑。

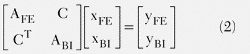

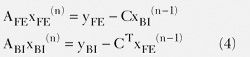

 举报
举报

 举报
举报

 举报
举报

