微波系统主要研究信号和能量两大问题:信号问题主要是研究幅频和相频特性;能量问题主要是研究能量如何有效地传输。微波系统是分布参数
电路,必须采用场分析法,但场分析法过于复杂,因此需要一种简化的分析方法。微波网络法被广泛运用于微波系统的分析,是一种等效电路法,在分析场分布的基础上,用路的方法将微波
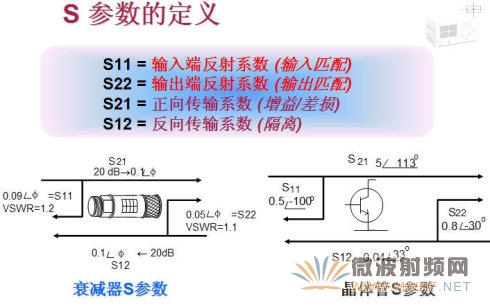
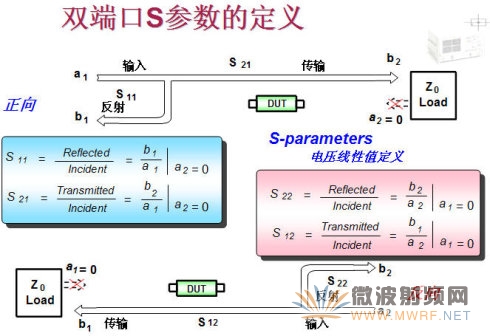
元件等效为电抗或电阻器件,将实际的导波传输系统等效为传输线,从而将实际的微波系统简化为微波网络,把场的问题转化为路的问题来解决。微波网络理论是在低频网络理论的基础上发展起来的,低频电路分析是微波电路分析的一个特殊情况。一般地,对于一个网络有Y、Z和S参数可用来测量和分析,Y称为导纳参数,Z称为阻抗参数,S称为散射参数;前两个参数主要用于集总电路,Z和Y参数对于集总参数电路分析非常有效,各参数可以很方便的测试;但是在微波系统中,由于确定非TEM波电压、电流非常困难,而且在微波频率测量电压和电流也存在实际困难。因此,在处理高频网络时,等效电压和电流以及有关的阻抗和导纳参数变得较抽象。与直接测量入射、反射及传输波概念更加一致的表示是散射参数,即S参数矩阵,它更适合于分布参数电路。S参数就是建立在入射波、反射波关系基础上的网络参数,适于微波电路分析,以器件端口的反射信号以及从该端口传向另一端口的信号来描述电路网络。同N端口网络的阻抗和导纳矩阵那样,用散射矩阵亦能对N端口网络进行完善的描述。阻抗和导纳矩阵反映了端口的总电压和电流的关系,而散射矩阵是反映端口的入射电压波和反射电压波的关系。散射参量可以直接用网络分析仪测量得到,可以用网络分析技术来计算。只要知道网络的散射参量,就可以将它变换成其它矩阵参量。


 举报
举报

 举报
举报

