在研究各种谐振
电路时,常常涉及到电路的品质因素Q值的问题,那末什么是Q值呢?下面我们作详细的论述。
1是一串联谐振电路,它由电容C、电感L和由电容的漏电阻与电感的线电阻R所组成。此电路的复数阻抗Z为三个
元件的复数阻抗之和。
Z=R+jωL+(-j/ωC)=R+j(ωL-1/ωC) ⑴
上式电阻R是复数的实部,感抗与容抗之差是复数的虚部,虚部我们称之为电抗用X表示, ω是外加信号的角频率。
当X=0时,电路处于谐振状态,此时感抗和容抗相互抵消了,即式⑴中的虚部为零,于是电路中的阻抗最小。因此电流最大,电路此时是一个纯电阻性负载电路,电路中的电压与电流同相。电路在谐振时容抗等于感抗,
所以电容和电感上两端的电压有效值必然相等,
电容上的电压有效值UC =I*1/ωC=U/ωCR=QU 品质因素Q=1/ωCR,这里I是电路的总电流。
电感上的电压有效值UL =ωLI=ωL*U/R=QU 品质因素Q=ωL/R
因为:UC =UL 所以Q=1/ωCR=ωL/R
电容上的电压与外加信号电压U之比UC /U= (I*1/ωC)/RI=1/ωCR=Q
电感上的电压与外加信号电压U之比UL /U= ωLI/RI=ωL/R=Q
从上面分析可见,
电路的品质因素越高,电感或电容上的电压比外加电压越高 。
电路的选择性:图1电路的总电流I=U/Z=U/[R2 +(ωL-1/ωC)2 ]1/2 =U/[R2 +(ωLω0 /ω0 -ω0 /ωCω0 )2 ]1/2 ω0 是电路谐振时的角频率。当电路谐振时有:ω0 L=1/ω0 C
所以I=U/{R2 +[ω0 L(ω/ω0 -ω0 /ω)]2 }1/2 = U/{R2 +[R2 (ω0 L/R)2 ](ω/ω0 -ω0 /ω)2 }1/2 = U/R[1+Q2 (ω/ω0-ω0/ω)2 ]1/2
因为电路谐振时电路的总电流I0 =U/R, 带入上式,有:
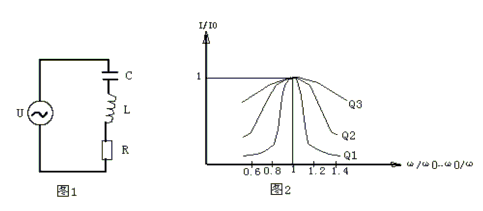
I=I0 /[1+Q2 (ω/ω0 -ω0 /ω)2 ]1/2 有:I/I0=1/[1+Q2 (ω/ω0 -ω0 /ω)2 ]1/2 作此式的函数曲线。
设(ω/ω0 -ω0 /ω)2 =Y
曲线如图2所示。这里有三条曲线,对应三个不同的Q值,其中有Q1>Q2>Q3。从图中可看出当外加信号频率ω偏离电路的谐振频率ω0 时, I/I0 均小于1。Q值越高在一定的频偏下电流下降得越快,其谐振曲线越尖锐。也就是说电路的选择性是由电路的品质因素Q所决定的,Q值越高选择性越好。



