基于LTCC技术的3-D超材料制造与设计

I．介绍
在1952年，Schelkunoff和Friis[1]提出由于人工介质的磁导率持续增长，应该使用开环谐振器（SRR）。尽管他们提出了磁导率方程，但是在讨论介电常数和磁导率的结果被否决后，他们没有这么做。在1968年，Veselago[2]提出在不违反麦克斯韦方程和坡印廷定理的情况下，材料可能具有小于1甚至是负的介电常数和磁导率。看来，这个文件被忽视了近30年，直到Shelby，Smith和Schultz[3]通过制造一个有拆分环和细线结构的样品，这个样品在微波的频率下的楔形容器内展示出了负折射，从而实验式地验证了Veselago的假说。Pendry和同事们[4]的开创性论文给了他们的实验工作很多的援助[5]。在他们的第一篇论文中，Pendry等人描述了在有效媒介的介电常数低于等离子体频率的情况下，周期性分布非常薄（小于0.01 λ）的电线是如何能引起类似血浆的行为，这取决于电线的宽度和间距以及介质嵌入的位置。在他们的第二篇论文中，他们描述了如何电动小分裂环的周期分布（约为0.1λ）可以产生一个有效的媒介，具有高度色散磁导率，在等效LC电路的共振频率下可以成为负的。超材料的名称被用来形容不寻常的这些材料的频率响应，前缀“meta”在希腊字中，意思是“超越”[6]。在过去10年中，在超材料领域的研究已发生爆炸，数以百计的论文已经发表，其中大部分的理论提出超材料使用于各种微波和光学应用[7]–[12]。
我们用Schelkunoff和Friis使用过的方法，来获得用RLC等效电路模型收集的小SRR的磁导率。如果入射磁场是垂直的SRR平面，感应电流的流经循环可以用下公式表示：
（1）
其中ω为频率，S是环路面积，Ho 为磁场的振幅，L是等效电感的SRR和C是电容的SRR的间隙，C是SRR间隙的电容。如果SRR是小电气性的，则等效磁偶极矩的SRR可写为Pm =IS。这类SRR集合的磁化强度（每单位体积的磁偶极矩）可以写作：
（2）
其中 是第i个类型单位的SRR数量，Xm 是磁化率，μ是超材料的有效磁导率。通过带入（1）中感应电流的表达式，我们可以写出SRR的电感L、电容C和电阻R的有效磁导率。如下：
（3）
我们观察到，当该场的频率与电路的共振频率 =1/LC一致，我们可以得到一个大的磁导率值。因此磁超材料的透气性，完全由于共振影响。远离共振区域，超材料是无磁性的。等效电感L和电容C可以用不用的SRR几何模型来算出。我们看到，这个简单的推导，可以用感应电流的概念给出一个超材料的磁导率表达式，这与许多作者所用的Lorentz模型相同。通常被写作
（4）
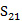我们把复介电常数和磁导率各自定义为ε' ±jε'' 和μ '''' '±jμ ''。物理学家更喜欢正号，而电气工程师更喜欢负号。绝大多数的自然材料 ε ＞0，μ ＞0。金属在光频段ε  ＜0，μ ＜0。抗磁材料ε  ＞0，μ ＜1。所有的超材料在共振频率，表现出高度分散行为。在共振频率，传输（ ）始终是一个最小值，伴随着在附近频率下的反射最小值。根据共振的强度和性质，介电常数的实部、磁导率的实部，或者两者一起，都能是负的。用Nicholson–Ross–Weir方法提取的介电常数和磁导率保证了材料是无源的，即复阻抗的实部是正的，波数的虚部导致了波在介质中的衰减。我们避免说明虚部是正的或是负的，由于虚部的正号或负号复属性定义导致的可变性。当我们进一步得到介电常数的虚部和磁导率，超材料拥有的介电常数和磁导率有正值和负值。对于普通的介质材料，介电常数的虚部将满足条件的因果关系。这对于负介电常数和负磁导率来实现负折射率是不是必须的。
微波异向介质的实验表征，和平面超材料测量的S参数的提取出的复介电常数和磁导率是由Varadan和Tellakula完成的[13]。图1显示的SRR是一个电小差距的细线环。这种SRR结构可以导致电场和磁场的共振。当环轴与H场平行，SRR的H场产生电流，从而引起强大的磁偶极子，因此磁共振。如果SRR的间隙与E 场平行，E场在间隙中产生一个变化的电压，导致了一个强大的磁偶极子，这会引起电谐振。对于一对对称的SRR，磁共振受激，两个SRR的磁偶极子应该加起来，而电偶极矩相互抵消[14]。对于电谐振，两个电偶极子应该加起来，而磁偶极子抵消。

图1 拆分环谐振器
在以前的实验工作[3]，[13]-[19]，印刷电路板（PCB）技术和湿法刻蚀被用来沉积介质基片等金属的共振结构例如FR4及Duroid。这些样本可用于平面传输线样品，其中波的传播可以是在平面结构上或是垂直于平面结构。打个比方，这些在[3]和[13]中用的样品，不能被用于实际应用。在本文中，对于3-D互连的超材料制造的低温共烧陶瓷（LTCC），表现出的每种设计规范所表现出的超材料色散现象，我们提出了一种设计方法。LTCC工艺被广泛用于工业微波和电子电路的封装，多层电路技术，并用于方便嵌入无源器件，如电感，电容和电阻。它可以封装提供的3-D电气连接中间层，其中在所需的位置用金属填充微通孔，这种能力也是很有吸引力的。LTCC工艺特别适合制作高频系统启动的封装，用于天线阵列，单片微波集成电路（MMIC）等[21]-[24]。
LTCC工艺可以成功地用于3-D超材料的制造，并提供了很大的改善和很多的功能功能，相对于目前的用PCB平版印刷技术制造的2-D超材料方法。对于MMIC的应用，结合基板上无源但共振的超材料结构将有几个优点。超材料的LTCC基板可以用来控制电磁干扰，并为内部的高频元件和外部的干扰源提供隔离和条块分割。
据我们所知，这是第一次系统地应用LTCC工艺来设计，制造和表征/验证用于毫米波的超材料。在本文中，我们首先描述与LTCC制造步骤相匹配的3-D超材料制造的设计过程，以及将这个设计与2-D超材料相比较。然后，我们描述了这种使用Ansoft公司的高频结构仿真（HFSS）的商业代码的全波仿真的电磁建模结构。在数字化设计中，我们计算了一块LTCC超材料板的S参数期望，和在烧制工艺中的收缩率期望。对于一些样品，计算出的S参数被用来抽取超材料的介电常数和磁导率。这种设计后来使用自由空间测量系统而被制造和实验特征化[13]。

图2 杜邦951基板上的2-D SRR单元
将仿真和测量数据进行了比较，两者符合得非常好。我们也提出了一种常用LTCC基板的复介电常数，杜邦951生瓷带（ =7.4−j0.026， =1）的频率范围为5.8–110GHz。这个数据对于其他研究人员在其设计中使用杜邦951是非常有用的。
LTCC工艺对于超材料制作是一个非常容易和成本效益的方法。它是一个容易被封装行业所接受的工艺，现在也在快速增长的超材料领域中有很好的应用。